벡터(Vector) 합,차

지금 부터 나온 벡터의 연산들은 기하적으로 설명으로 좌표 평면이나 좌표 공간에서

위치벡터들의 연산를 설명할 것입니다.


벡터의 크기

벡터의 크기를 구할때 피타고라스의 정리를 이용하는데

시점이 원점(O)이고  점A (a1,a2)에 대한 벡터의 크기는 각 성분의 제곱에 루트를 씌운 것입니다.

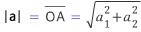
벡터OA의 스칼라의 양이기도 합니다.


시점이 원점을 지나지 않는 경우에도 피타고라스 정리를 이용하는데요

저 파란벡터가 시작되는 시점을 P   끝나는 종점을 Q라고 하면 벡터 PQ는 

가됩니다.

벡터의 합,차

한 소년이 새총으로 돌을 쏘았을때 돌에  작용 하는 힘은 어떻게 될까요?

그림은 새총을 위에서 본모습입니다..

두줄의 고무줄과 돌을 감쌀수 있는 가죽부분 그리고 돌로 구성되어있습니다..

가죽부분을 손가락으로 잡고 뒤로 당겼을 경우 두줄의 고무줄에 장력이 생기게 됩니다.

어느정도 장력이 생기고 손가락을 놓았을 경우 두줄의 장력의 힘이 돌맹이에게 전달됩니다..

이런 경우 벡터의 합연산으로 돌맹이가 받는 힘의 방향과 크기를 알수 있게 됩니다.

이런 벡터의 합을 좌표로 표현하게되면 이렇게 됩니다.

기학적으로 보시면 벡터 a의 종점에  벡터 b의 시작점을 놓은 모양이 됩니다.

두변의 벡터a,벡터b로 이루어지는  대각선이 벡터r인 평행 사변형이 됩니다.

결과벡터는 각 벡터의 성분끼리 더하면 결과값이 나오게 되어있습니다.

벡터의 차는 각 벡터의 성분끼리 빼주면 결과값이 나오게 되어있습니다.

두 벡터  벡터A(-5,7)  , 벡터B(10,10)의 차는 벡터 C( -5 - 10 , 7 - 10) = 벡터C(-15, -3)이 됩니다.

결과는 대각선 변이 벡터A이고 벡터C와 벡터B가 변인 평행 사변형 모양이 됩니다.

벡터A - 벡터B = 벡터C 라는 벡터간의 관계가 있다면 다음 그림과 같이 그려도 무관합니다.

벡터는 평행으로 옮겨져도 크기와 방향이 같기 때문입니다.

지금까지 2차원 직교좌표에서 설명을 드렸는데 3차원에서도 성분(z)이 추가될뿐 

방식은 마찬가지입니다.